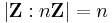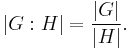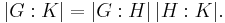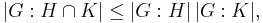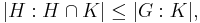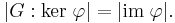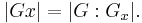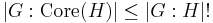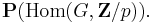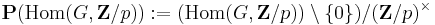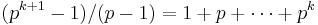Index of a subgroup

In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" (cosets) of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H. The index of H in G is usually denoted |G : H| or [G : H].

Formally, the index of H in G is defined as the number of cosets of H in G. (The number of left cosets of H in G is always equal to the number of right cosets.) For example, let Z be the group of integers under addition, and let 2Z be the subgroup of Z consisting of the even integers. Then 2Z has two cosets in Z (namely the even integers and the odd integers), so the index of 2Z in Z is two. In general,

$|\mathbf{Z}:n\mathbf{Z}| = n$

for any positive integer n.

If N is a normal subgroup of G, then the index of N in G is also equal to the order of the quotient group G / N, since this is defined in terms of a group structure on the set of cosets of N in G.

If G is infinite, the index of a subgroup H will in general be a cardinal number. It may however be finite, that is, a positive integer, as the example above shows.

If G and H are finite groups, then the index of H in G is equal to the quotient of the orders of the two groups:

$|G:H| = \frac{|G|}{|H|}.$

This is Lagrange's theorem, and in this case the quotient is necessarily a positive integer.

1 Properties
2 Examples
3 Infinite index
4 Finite index
- 4.1 Proof
- 4.2 Examples
5 Normal subgroups of prime power index
- 5.1 Geometric structure
6 See also
7 References
8 External links

Properties

If H is a subgroup of G and K is a subgroup of H, then

$|G:K| = |G:H|\,|H:K|.$

If H and K are subgroups of G, then

$|G:H\cap K| \le |G�: H|\,|G�: K|,$

with equality if HK = G. (If |G : H ∩ K| is finite, then equality holds if and only if HK = G.)

Equivalently, if H and K are subgroups of G, then

$|H:H\cap K| \le |G:K|,$

with equality if HK = G. (If |H : H ∩ K| is finite, then equality holds if and only if HK = G.)

If G and H are groups and φ: G → H is a homomorphism, then the index of the kernel of φ in G is equal to the order of the image:

$|G:\operatorname{ker}\;\varphi|=|\operatorname{im}\;\varphi|.$

Let G be a group acting on a set X, and let x ∈ X. Then the cardinality of the orbit of x under G is equal to the index of the stabilizer of x:

$|Gx| = |G:G_x|.\!$

This is known as the orbit-stabilizer theorem.

As a special case of the orbit-stabilizer theorem, the number of conjugates gxg⁻¹ of an element x ∈ G is equal to the index of the centralizer of x in G.
Similarly, the number of conjugates gHg⁻¹ of a subgroup H in G is equal to the index of the normalizer of H in G.
If H is a subgroup of G, the index of the normal core of H satisfies the following inequality:

$|G:\operatorname{Core}(H)| \le |G:H|!$

where ! denotes the factorial function; this is discussed further below.

As a corollary, if the index of H in G is 2, or for a finite group the lowest prime p that divides the order of G, then H is normal, as the index of its core must also be p, and thus H equals its core, i.e., is normal.
Note that a subgroup of lowest prime index may not exist, such as in any simple group of non-prime order, or more generally any perfect group.

Examples

The alternating group 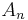$A_n$ has index 2 in the symmetric group 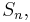$S_n,$ and thus is normal.
The special orthogonal group SO(n) has index 2 in the orthogonal group O(n), and thus is normal.
The free abelian group Z ⊕ Z has three subgroups of index 2, namely

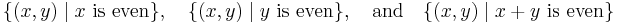$\{(x,y) \mid x\text{ is even}\},\quad \{(x,y) \mid y\text{ is even}\},\quad\text{and}\quad \{(x,y) \mid x%2By\text{ is even}\}$ .

More generally, if p is prime then Zⁿ has (pⁿ − 1) / (p − 1) subgroups of index p, corresponding to the pⁿ − 1 nontrivial homomorphisms Zⁿ → Z/pZ.
Similarly, the free group F_n has pⁿ − 1 subgroups of index p.
The infinite dihedral group has a cyclic subgroup of index 2, which is necessarily normal.

Infinite index

If H has an infinite number of cosets in G, then the index of H in G is said to be infinite. In this case, the index |G : H| is actually a cardinal number. For example, the index of H in G may be countable or uncountable, depending on whether H has a countable number of cosets in G. Note that the index of H is at most the order of G, which is realized for the trivial subgroup, or in fact any subgroup H of infinite cardinality less than that of G.

Finite index

An infinite group G may have subgroups H of finite index (for example, the even integers inside the group of integers). Such a subgroup always contains a normal subgroup N (of G), also of finite index. In fact, if H has index n, then the index of N can be taken as some factor of n!.

A special case, n = 2, gives the general result that a subgroup of index 2 is a normal subgroup, because the normal group (N above) must have index 2 and therefore be identical to the original subgroup. More generally, a subgroup of index p where p is the smallest prime factor of the order of G (if G is finite) is necessarily normal, as the index of N divides p! and thus must equal p, having no other prime factors.

This result is generally proven using group actions; an alternative proof of the result that subgroup of index lowest prime p is normal, and other properties of subgroups of prime index are given in (Lam 2004).

Proof

This can be seen more concretely, by considering the permutation action of G on left cosets of H when multiplying them on the right by elements of G (or, equally, multiplying right cosets on the left). This provides a quotient group of G, the image of this permutation representation, which is a subgroup of the symmetric group on n elements.

Let us explain this now in more detail. The elements of G that leave all cosets the same form a group.

(If Hca ⊂ Hc ∀ c ∈ G and likewise Hcb ⊂ Hc ∀ c ∈ G, then Hcab ⊂ Hc ∀ c ∈ G. If h₁ca = h₂c for all c ∈ G (with h₁, h₂ ∈ H) then h₂ca⁻¹ = h₁c, so Hca⁻¹ ⊂ Hc.)

Let us call this group A. Let B be the set of elements of G which perform a given permutation on the cosets of H. Then the cardinality (size) of B is equal to the cardinality of A, and in fact B is a right coset of A.

(If cb₁ = d and cb₂ = hd (a member of the same coset as d), then cb₁b₂⁻¹ = db₂⁻¹ = h⁻¹c ∈ Hc. Since this is the case for any b₂ and for any c (with appropriate d), b₁b₂⁻¹ ∈ A and the size of B is less than or equal to the size of A. Conversely, Hcb₁ = Hcab₁, and since the left-hand side is in Hd then so is the right-hand side: Hcab₁ ⊂ Hcd, showing that for any element of A there is a different element of B, and thus the size of A is less than or equal to the size of B.)

Since the number of possible permutations of cosets is finite, namely n! (assuming H is of finite index n), then there can only be a finite number of sets like B. If G is infinite, then all such sets are therefore infinite. The set of these sets forms a group isomorphic to a subset of the group of permutations, so the number of these sets must divide n!. Finally, if for some c ∈ G and a ∈ A we have ca = xc, then for any d ∈ G dca = hdc for some h ∈ H, but also dca = dxc, so hd = dx. Since this is true for any d, x must be a member of A, so ca = xc implies that A is a normal subgroup.

Examples

The above considerations are true for finite groups as well. For instance, the group O of chiral octahedral symmetry has 24 elements. It has a dihedral D₄ subgroup (in fact it has three such) of order 8, and thus of index 3 in O, which we shall call H. This dihedral group has a 4-member D₂ subgroup, which we may call A. Multiplying on the right any element of a right coset of H by an element of A gives a member of the same coset of H (Hca = Hc). A is normal in O. There are six cosets of A, corresponding to the six elements of the symmetric group S₃. All elements from any particular coset of A perform the same permutation of the cosets of H.

On the other hand, the group T_h of pyritohedral symmetry also has 24 members and a subgroup of index 3 (this time it is a D_2h prismatic symmetry group, see point groups in three dimensions), but in this case the whole subgroup is a normal subgroup. All members of a particular coset carry out the same permutation of these cosets, but in this case they represent only the 3-element alternating group in the 6-member S₃ symmetric group.

Normal subgroups of prime power index

Normal subgroups of prime power index are kernels of surjective maps to p-groups and have interesting structure, as described at Focal subgroup theorem: Subgroups and elaborated at focal subgroup theorem.

There are three important normal subgroups of prime power index, each being the smallest normal subgroup in a certain class:

E^p(G) is the intersection of all index p normal subgroups; G/E^p(G) is an elementary abelian group, and is the largest elementary abelian p-group onto which G surjects.
A^p(G) is the intersection of all normal subgroups K such that G/K is an abelian p-group (i.e., K is an index 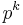$p^k$ normal subgroup that contains the derived group $[G,G]$ ): G/A^p(G) is the largest abelian p-group (not necessarily elementary) onto which G surjects.
O^p(G) is the intersection of all normal subgroups K of G such that G/K is a (possibly non-abelian) p-group (i.e., K is an index 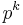$p^k$ normal subgroup): G/O^p(G) is the largest p-group (not necessarily abelian) onto which G surjects. O^p(G) is also known as the p-residual subgroup.

As these are weaker conditions on the groups K, one obtains the containments

$\mathbf{E}^p(G) \supseteq \mathbf{A}^p(G) \supseteq \mathbf{O}^p(G).$

These groups have important connections to the Sylow subgroups and the transfer homomorphism, as discussed there.

Geometric structure

An elementary observation is that one cannot have exactly 2 subgroups of index 2, as the complement of their symmetric difference yields a third. This is a simple corollary of the above discussion (namely the projectivization of the vector space structure of the elementary abelian group

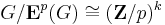$G/\mathbf{E}^p(G) \cong (\mathbf{Z}/p)^k$ ),

and further, G does not act on this geometry, nor does it reflect any of the non-abelian structure (in both cases because the quotient is abelian).

However, it is an elementary result, which can be seen concretely as follows: the set of normal subgroups of a given index p form a projective space, namely the projective space

$\mathbf{P}(\operatorname{Hom}(G,\mathbf{Z}/p)).$

In detail, the space of homomorphisms from G to the (cyclic) group of order p, 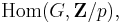$\operatorname{Hom}(G,\mathbf{Z}/p),$ is a vector space over the finite field 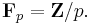$\mathbf{F}_p = \mathbf{Z}/p.$ A non-trivial such map has as kernel a normal subgroup of index p, and multiplying the map by an element of 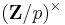$(\mathbf{Z}/p)^\times$ (a non-zero number mod p) does not change the kernel; thus one obtains a map from

$\mathbf{P}(\operatorname{Hom}(G,\mathbf{Z}/p))�:= (\operatorname{Hom}(G,\mathbf{Z}/p))\setminus\{0\})/(\mathbf{Z}/p)^\times$

to normal index p subgroups. Conversely, a normal subgroup of index p determines a non-trivial map to 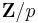$\mathbf{Z}/p$ up to a choice of "which coset maps to 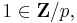$1 \in \mathbf{Z}/p,$ which shows that this map is a bijection.

As a consequence, the number of normal subgroups of index p is

$(p^{k%2B1}-1)/(p-1)=1%2Bp%2B\cdots%2Bp^k$

for some k; 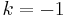$k=-1$ corresponds to no normal subgroups of index p. Further, given two distinct normal subgroups of index p, one obtains a projective line consisting of 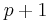$p%2B1$ such subgroups.

For 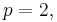$p=2,$ the symmetric difference of two distinct index 2 subgroups (which are necessarily normal) gives the third point on the projective line containing these subgroups, and a group must contain 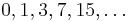$0,1,3,7,15,\ldots$ index 2 subgroups – it cannot contain exactly 2 or 4 index 2 subgroups, for instance.

References

Lam, T. Y. (March 2004), "On Subgroups of Prime Index", The American Mathematical Monthly 111 (3): 256–258, JSTOR 4145135, alternative download

Index of a subgroup

Contents

Properties

Examples

Infinite index

Finite index

Proof

Examples

Normal subgroups of prime power index

Geometric structure

See also

References

External links